Parent Functions And Transformations Calculator

Parent Functions – Types, Backdrop & Examples

When working with functions and their graphs, yous'll notice how virtually functions' graphs look akin and follow similar patterns. That'southward considering functions sharing the same degree will follow a like curve and share the same parent functions.

A parent function represents a family of functions' simplest class.

This definition perfectly summarizes what parent functions are. We utilize parent functions to guide us in graphing functions that are establish in the same family. In this article, we volition:

Review all the unique parent functions (you might have already encountered some before).
Learn how to identify the parent function that a function belongs to.

Existence able to identify and graph functions using their parent functions tin can help the states empathise functions more, and then what are we waiting for?

What is a parent function?

Now that we understand how important it is for us to master the unlike types of parent functions allow's first start to understand what parent functions are and how their families of functions are afflicted by their backdrop.

Parent office definition

Parent functions are the simplest form of a given family unit of functions. A family of functions is a group of functions that share the same highest degree and, consequently, the same shape for their graphs.

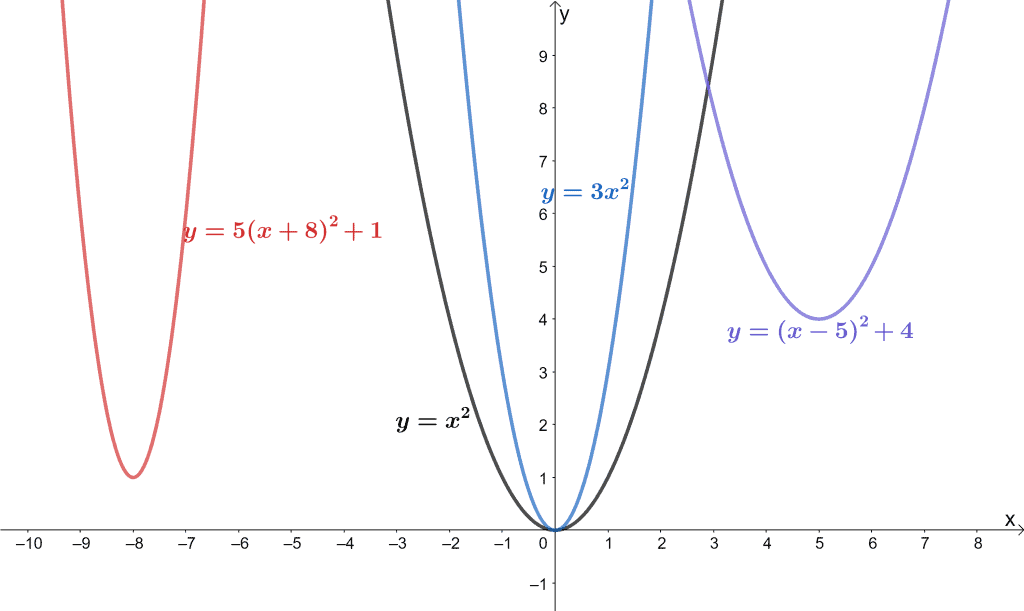
The graph in a higher place shows iv graphs that showroom the U-shaped graph we phone call the parabola. Since they all share the same highest degree of two and the same shape, we can group them as one family of office. Can you guess which family do they vest to?

These four are all quadratic functions, and their simplest grade would be y = x². Hence, the parent office for this family is y = x².

Since parent functions are the simplest form of a given grouping of functions, they tin can immediately give you an idea of how a given function from the same family would look like.

What are the different types of parent functions?

It's now fourth dimension to refresh our knowledge about functions and also learn most new functions. As we accept mentioned, familiarizing ourselves with the known parent functions will help us empathize and graph functions ameliorate and faster.

Why don't we start with the ones that we might already have learned in the past?

The offset four parent functions involve polynomials with increasing degrees. Let'south observe how their graphs comport and have note of the respective parent functions' domain and range.

Abiding Functions

Abiding functions are functions that are defined past their respective constant, c. All constant functions will take a horizontal line equally its graph and comprise only a abiding as its term.

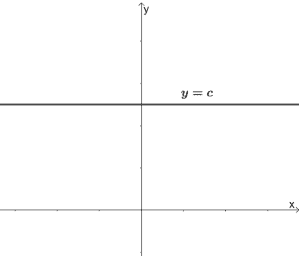
All constant functions will take all real numbers as its domain and y = c equally its range. They also each take a y-intercept at (0, c).

An object's motion when it is at rest is a expert example of a constant function.

Linear Functions

Linear functions have x as the term with the highest degree and a general form of y = a + bx. All linear functions have a straight line every bit a graph.

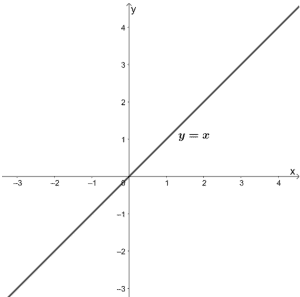
The parent office of linear functions is y = ten, and it passes through the origin. The domain and range of all linear functions are all real numbers.

These functions represent relationships between two objects that are linearly proportional to each other.

Quadratic Functions

Quadratic functions are functions with 2 as its highest degree. All quadratic functions return a parabola as their graph. As discussed in the previous section, quadratic functions have y = x² every bit their parent function.

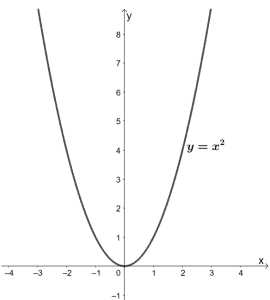
The vertex of the parent function y = x² lies on the origin. It also has a domain of all real numbers and a range of [0, ∞). Observe that this office increases when x is positive and decreases while x is negative.

A good application of quadratic functions is projectile motion. We can observe an object's projectile motion by graphing the quadratic function that represents it.

Cubic Functions

Let's move on to the parent function of polynomials with 3 every bit its highest degree. Cubic functions share a parent function of y = x³ . This function is increasing throughout its domain.

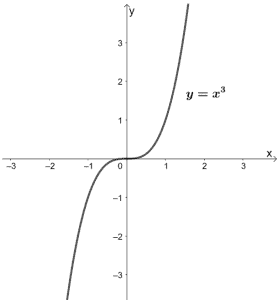
Every bit with the two previous parent functions, the graph of y = x³ also passes through the origin. Its domain and range are both (-∞, ∞) or all real numbers too.

Absolute Value Functions

The parent function of absolute value functions is y = |x|. Equally shown from the parent function'southward graph, accented value functions are expected to return V-shaped graphs.

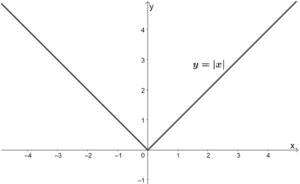
The vertex of y = |x| is constitute at the origin equally well. Since it extends on both ends of the x-centrality, y= |x| has a domain at (-∞, ∞). Accented values can never be negative, so the parent function has a range of [0, ∞).

We employ absolute value functions to highlight that a part's value must always be positive.

Radical Functions

The ii most ordinarily used radical functions are the square root and cube root functions.

The parent function of a square root function is y = √x. Its graph shows that both its 10 and y values can never be negative.

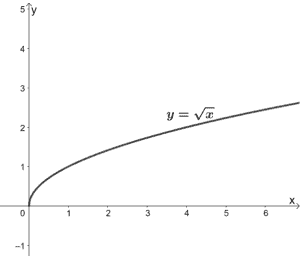
This ways that the domain and range of y = √x are both [0, ∞). The starting point or vertex of the parent part is also institute at the origin. The parent function y = √x is likewise increasing throughout its domain.

Let'southward now study the parent function of cube root functions. Similar to the square root function, its parent part is expressed as y = ∛ x.

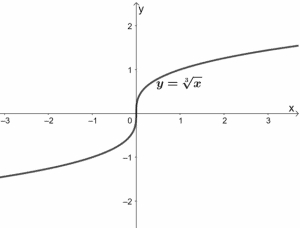
The graph shows that the parent office has a domain and range of (-∞, ∞). We can likewise come across that y = ∛x is increasing throughout its domain.

Exponential Functions

Exponential functions are functions that take algebraic expressions in their exponent. Their parent function tin can be expressed as y = b^x , where b can be whatsoever nonzero abiding. The parent function graph, y = due east¹⁰, is shown beneath, and from information technology, we tin see that it will never exist equal to 0.

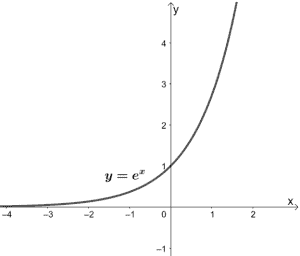
And when x = 0, y passing through the y-axis at y = i. We can also come across that the parent function is never establish beneath the y-axis, and then its range is (0, ∞). Its domain, all the same, tin be all real numbers. Nosotros can also see that this part is increasing throughout its domain.

1 of the most common applications of exponential functions is modeling population growth and compound interest.

Logarithmic Functions

Logarithmic functions are the changed functions of exponential functions. Its parent role tin be expressed equally y = log_b x, where b is a nonzero positive abiding. Let'due south notice the graph when b = 2.

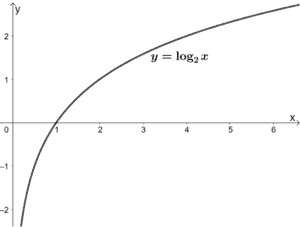
Like the exponential function, we can see that x can never be less than or equal to goose egg for y = log₂x. Hence, its domain is (0,∞). Its range, yet, contains all existent numbers. We tin can as well see that this office is increasing throughout its domain.

Nosotros apply logarithmic functions to model natural phenomena such as an earthquake's magnitude. We too use it when calculating the half-life decay rate in physics and chemistry.

Reciprocal Functions

Reciprocal functions are functions that contain a constant numerator and x equally its denominator. Its parent function is y = 1/x.

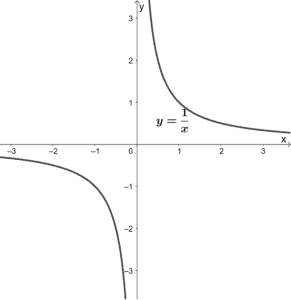
As can be seen from its graph, both x and y tin can never be equal to zero. This means that its domain and range are (-∞, 0) U (0, ∞). We tin can also see that the function is decreasing throughout its domain.

At that place are many other parent functions throughout our journeying with functions and graphs, just these eight parent functions are that of the almost commonly used and discussed functions.

You tin even summarize what you've learned so far by creating a table showing all the parent functions' backdrop.

How to find the parent role?

What if nosotros're given a function or its graph, and we need to identify its parent part? We can do this past remembering each function'due south important properties and identifying which of the parent graphs we've discussed lucifer the one that's given.

Here are some guide questions that tin assist us:

What is the part's highest degree?
Does it contain a square root or cube root?
Is the function found at the exponent or denominator?
Is the function's graph decreasing or increasing?
What is the function'due south domain or range?

If we can answer some of these questions by inspection, nosotros volition exist able to deduce our options and eventually identify the parent function.

Let's endeavor f(x) = 5(10 – 1)². We can see that the highest caste of f(x) is 2, so nosotros know that this function is a quadratic function. Hence, its parent role is y = xⁱⁱ .

Why don't we graph f(x) and ostend our reply every bit well?

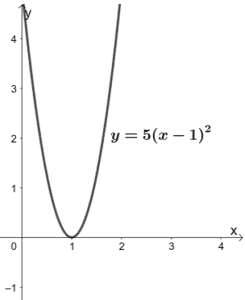
From the graph, we can see that it forms a parabola, confirming that its parent function is y = xⁱⁱ.

Review the outset few sections of this commodity and your own notes, and then let'southward try out some questions to check our knowledge on parent functions.

Example i

Graphs of the five functions are shown below. Which of the following functions do not belong to the given family of functions?

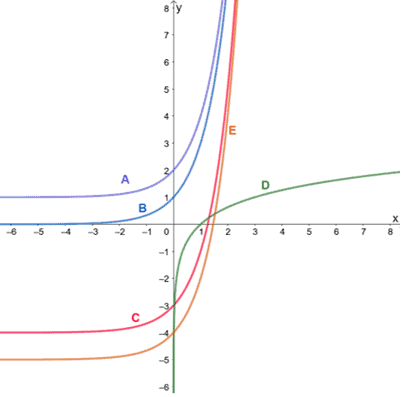
Solution

The functions represented past graphs A, B, C, and E share a similar shape just are either translated upward or downward. In fact, these functions represent a family unit of exponential functions. This means that they also all share a common parent function: y=b^x.

On the other hand, the graph of D represents a logarithmic function, and so D does non vest to the group of exponential functions.

Example 2

Which of the following functions do not belong to the given family of functions?

y = 5x²
y = -2x² + 3x – 1
y = x(3xⁱⁱ)
y = (x – 1)(10 + 1)

Solution

The function y = 5x² has the highest degree of two, so it is a quadratic role. This means that its parent part is y = ten^two. The same goes for y = -2x² + 3x – 1. From this, nosotros tin confirm that we're looking at a family of quadratic functions.

Applying the divergence of perfect squares on the quaternary option, nosotros take y = xⁱⁱ – 1. This is besides a quadratic function. That leaves us with the third option.

When expanded, y = x(3x²) becomes y = 3x^3, and this shows that it has iii as its highest degree. Hence, information technology tin't be office of the given family unit of functions.

Example 3

Identify the parent part of the post-obit functions based on their graphs. Ascertain each function's domain and range as well.

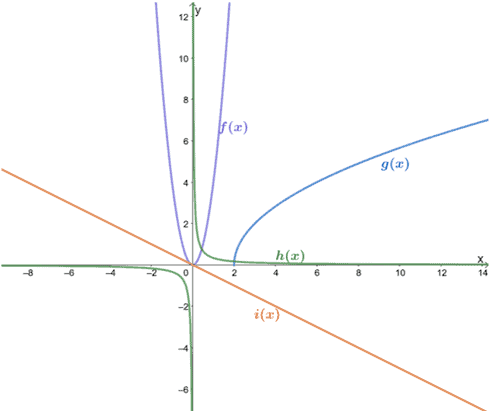
Solution

Let'due south showtime with f(x). Nosotros can encounter that it has a parabola for its graph, so we can say that f(x) is a quadratic function.

This means that f(x) has a parent function of y = x² .
The graph extends on both sides of x, so information technology has a domain of (-∞, ∞).
The parabola never goes below the ten-centrality, so it has a range of [0,∞).

Based on the graph, nosotros can see that the ten and y values of m(x) volition never be negative. They also bear witness an increasing curve that resembles the graph of a square root function.

Hence, the parent function of g(10) is y = √ten.
The graph extends to the right side of x and is never less than 2, and so it has a domain of [ii, ∞).
The parabola never goes below the x-axis, and so it has a range of [0,∞).

The h(ten) graph shows that their x and y values will never exist equal to 0. The symmetric curves besides look like the graph of reciprocal functions.

This means that h(x) has a parent role of y = 1/x.
Equally long equally the 10 and y are never equal to zero, h(x) is yet valid, and so it has both a domain and range of (-∞, ∞).

The straight lines representing i(x) tells that information technology is a linear function.

It has a parent part of y = x.
The graph extends on both sides of 10 and y, and so information technology has a domain and range of (-∞, ∞).

Example four

Place the parent office of the following functions.

f(ten) = x³ – 2x + ane
thousand(10) = 3√x + one
h(x) = 4/ x
i(x) = e ^{x + ane}

Solution

The highest degree of f(ten) is 3, so it's a cubic office. This ways that information technology has a parent office of y = x^three .
The function 1000(x) has a radical expression, 3√x. Since it has a term with a square root, the office is a square root function and has a parent part of y = √x.
Nosotros tin run into that ten is institute at the denominator for h(x), so it is reciprocal. Hence, its parent function is y = 1/x.
The function'south exponents contain x, so this alone tells u.s.a. that i(ten) is an exponential office. Hence, its parent function can be expressed as y = b^x, where b is a constant. For the case of i(10), nosotros have y = e^x as its parent role.